Lab Session #8 #
Agenda #
- Non-deterministic FSA
- NDFSA to (D)FSA
- Regular Expressions (RegExp)
Non-deterministic Finite State Automata (NDFSA) #
Definition #
A NDFSA is a tuple \( \lang Q, I, \delta, q_0, F\rang \) , where \(Q, I, q_0, F \) are defined as in (D)FSA and the transition function is defined as
\[ \delta : Q \times I \to \mathbb{P}(Q) \]\( \mathbb{P} \) is the powerset function (i.e. set of all possible students)
A NDFSA modifies the definition of a FSA to permit transitions at each stage to either zero, one, or more than one states.
The extended transition δ* for NDFSA #
Let \( M = \lang Q, I, \delta, q_0, F\rang \) be a NDFSA. We define the extended transition function as follows:
- For every \( q \in Q\) , \( \delta^\ast(q,\epsilon) = \{q\}\)
- For every \( q \in Q\) , every \( y \in I^\ast\) , and every \( i \in I\) ,
Acceptance by a NDFSA #
Let \( M = \lang Q, I, \delta, q_0, F\rang \) be a NDFSA. and let \( x \in I^\ast \) . The string \( x \) is accepted by \( M \) if
\[ \delta^\ast(q_0,x)\cap F \neq \varnothing\]and it is rejected by \( M \) otherwise.
Notion: Among the various possible runs (with the same input) of the NDFSA, it is sufficient that one of them succeeds to accept the input string.
Exercises on NDFSA #
Build NDFSAs that recognise the following languages:
- \( L_a = \{x \in \{0, 1\}^* \mid x \) ends with \(101\} \) ;
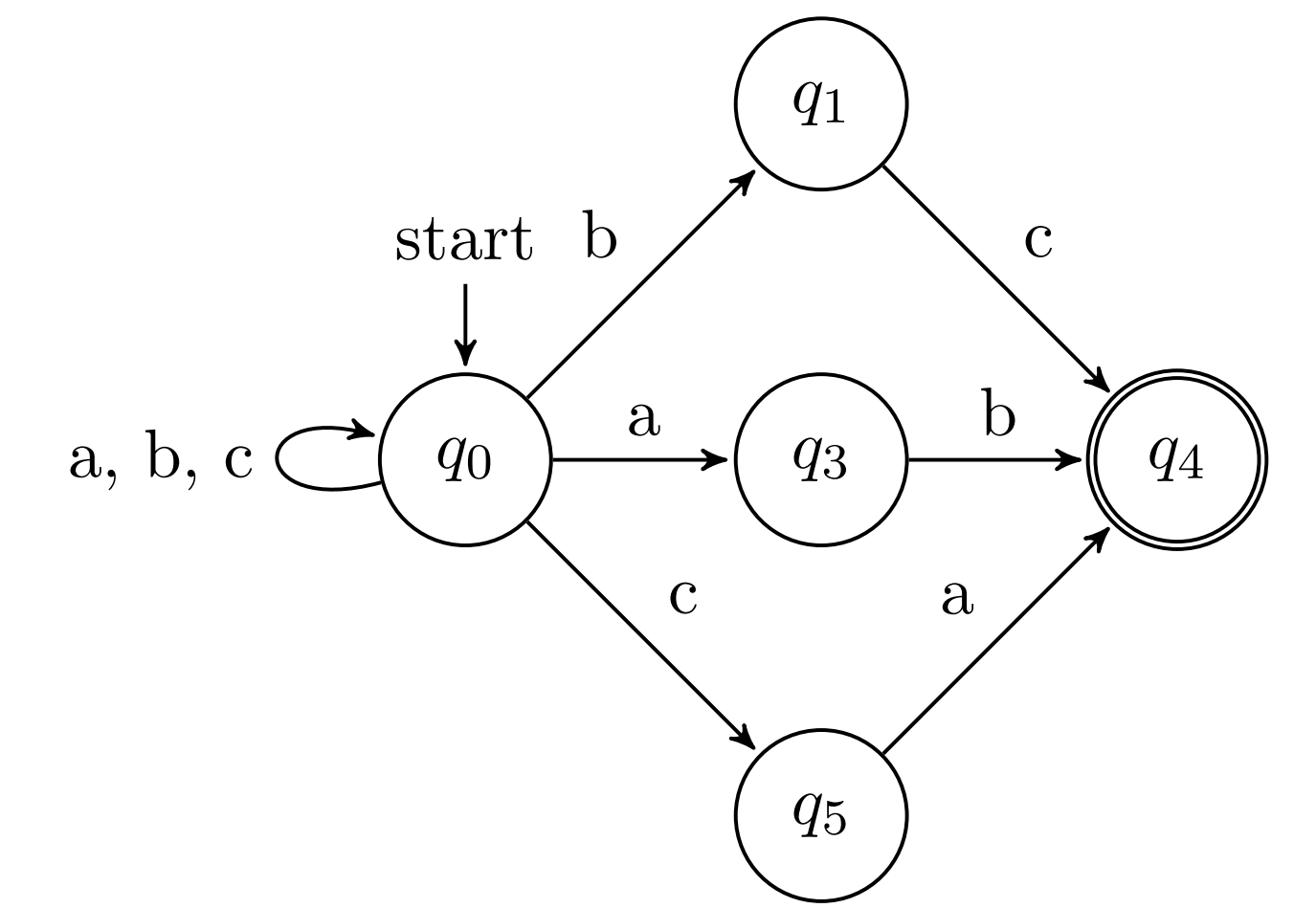
- \( L_b = \{xy \mid x \in \{a\}^* \wedge y \in \{a, b\}^* \wedge y \) does not start with \(\text{\textquoteleft}b\text{\textquoteright} \wedge \) every \(\text{\textquoteleft} a \text{\textquoteright}\) in \(y \) is followed by exactly one \(\text{\textquoteleft}b\text{\textquoteright}\} \) ;
- \( L_a = \{x \in \{a, b, c\}^* \mid x \) ends with either \(ab\) , \(bc\) or \(ca\}\) ;
NDFSA to DFSA #
Algorithm for NDFSA to DFSA #
- Create state table from the given NDFA
- Create a blank state table under possible input alphabets for the equivalent DFA
- Mark the start state of the DFA by \(q_0\) (Same as the NDFA)
- Find out the combination of States \(q_0, q_1, ..., q_n\) for each possible input alphabet
- Each time we generate a new DFA state under the input alphabet columns, we have to apply step \(4\) again, otherwise go to step \(6\)
- The states which contain any of the accepting states of the NDFA are the accepting states of the equivalent DFA
Simple example (1) #
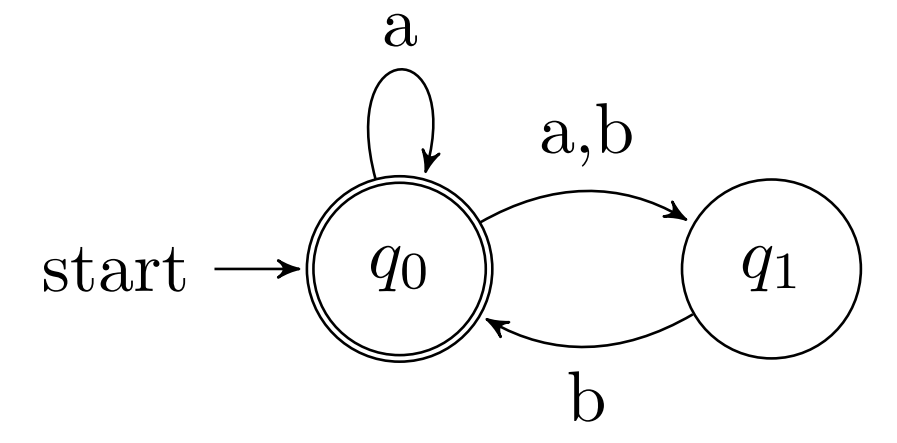
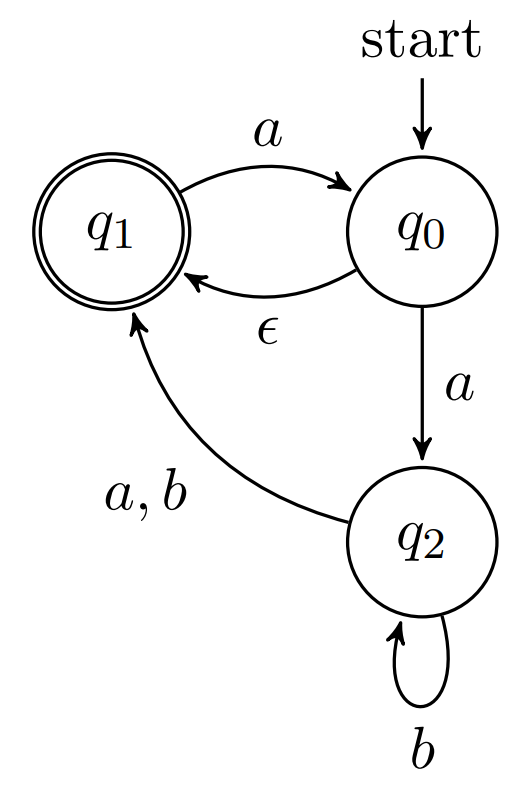
Example with steps #
Let us consider the following NDFSA:
First, we build a transition table for NDFSA:
Using table from previous step, let us create a similar table, but this time for FSA. Initially, the table is empty:
We begin by adding the initial state and the set of states:
The initial state can take us to two new states that are not yet in the table. Note that we treat a set of states as a single state now!
The next step is to find possible states for \(\{q_1,q_2\}\) and \(q_3\) . For \(q_3\) it is trivial, you just need to look it up in the original NDFSA table. However, the transition for \(\{q_1,q_2\}\) will be a union of sets: \[\delta({q_1,q_2},0) = \delta(q_1,0) \cup \delta(q_2,0) = \{q_3\} \] \[\delta({q_1,q_2},1) = \delta(q_1,1) \cup \delta(q_2,1) = \{q_0,q_1,q_3\}\]
Repeat the steps above until we have included all states from the original NDFSA and there are no new states.
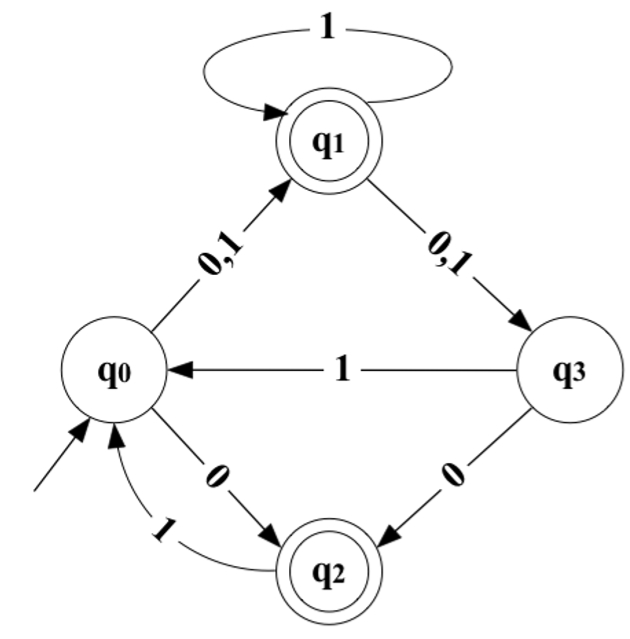
After repeating previous steps and depicting final states we will arrive to the following table:
The result will be the following:
Exercise 1 #
Build DFSA from the NDFSA that recognizes the language:
\( L_1 = \{x \in \{0, 1\}^* \mid x \) ends with \(101\} \) ;
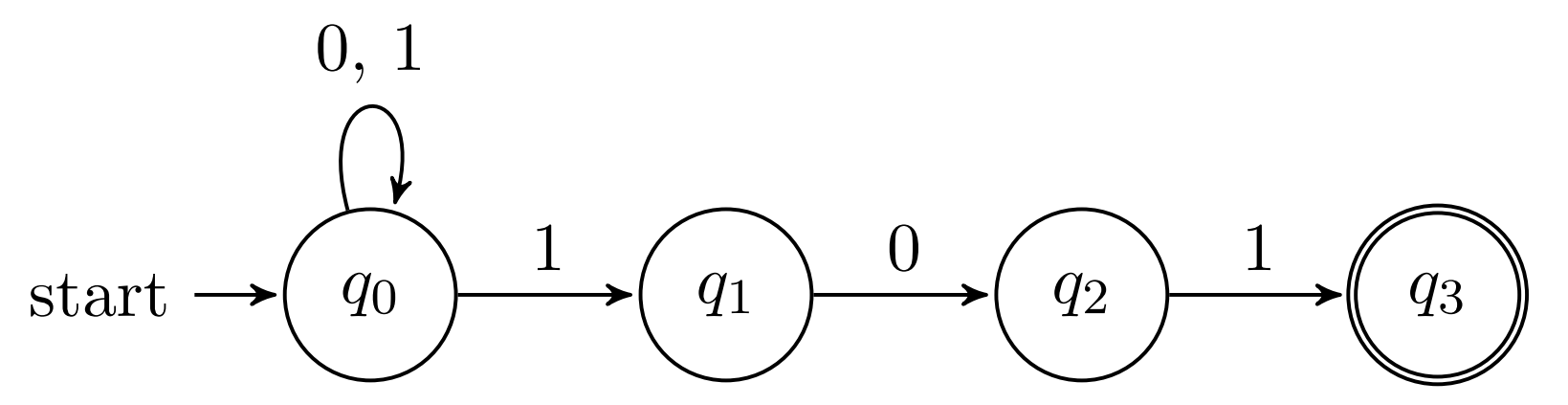
Exercise 2 #
Build DFSA from the NDFSA that recognizes the language:
\( L_2 = \{xy \mid x \in \{a\}^* \wedge y \in \{a, b\}^* \wedge y \) does not start with \(\text{\textquoteleft}b\text{\textquoteright} \wedge \) every \(\text{\textquoteleft} a \text{\textquoteright}\) in \(y \) is followed by exactly one \(\text{\textquoteleft}b\text{\textquoteright}\} \) ;
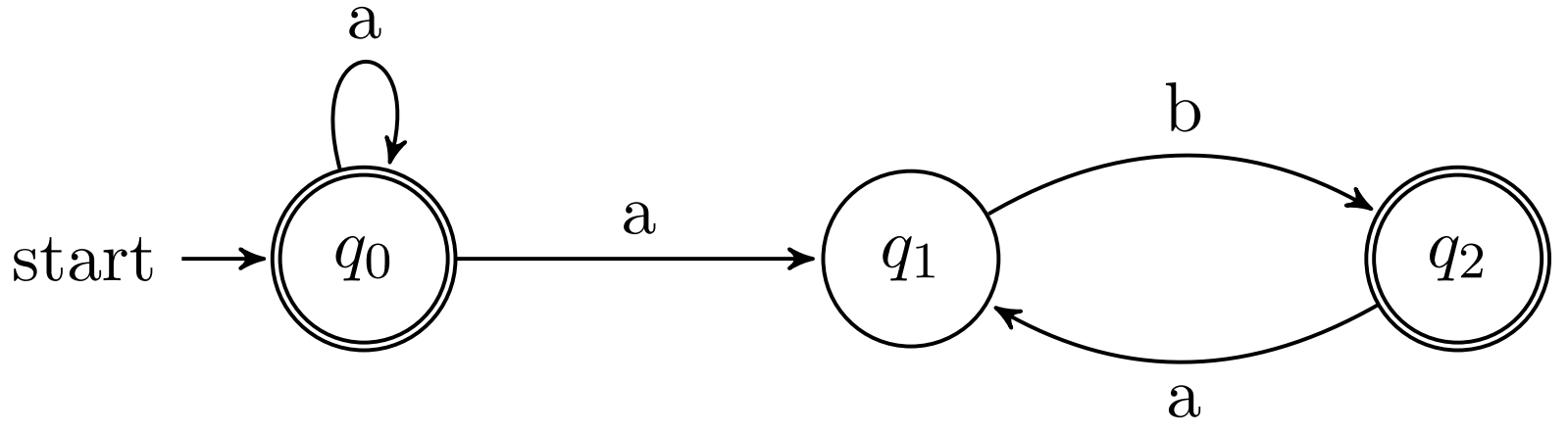
Exercise 3 #
Build DFSA from the NDFSA that recognizes the language:
\( L_3 = \{x \in \{a, b, c\}^* \mid x \) ends with either \(ab\) , \(bc\) or \(ca\}\) ;
Regular Expressions (RegExp) #
Definition #
Inductive definition of RegExps over an alphabet \(\Sigma\) : Basis.
- Symbol \(\emptyset\) is a regular expression (denoting the langauge \(\emptyset\) );
- Symbol \(\epsilon\) is a RegExp (denoting the language \(\{\epsilon\}\) );
- Each symbol \(\sigma\) of \(\Sigma\) is a RegExp
\(L(\sigma) = \{\sigma\}\) for each \(\sigma\in\Sigma\)
Induction. Let \(r\) and \(s\) be two RegExps, then
- \((r\cdot{s})\) is a RegExp (for simplicity, the dot is often omitted); \[L((r\cdot{s})) = \{ww'\mid(w \in L(r) \wedge w' \in L(s))\}\]
- \((r|s)\) is a RegExp \[L((r|s)) = L(r) \cup L(s)\]
- \(r^*\) is a RegExp \[L(r^*) = L(r)^*\]
If \(A\) and \(B\) are RegExp, then
- \(A\cdot{B} = \{xy\text{\textbar}x \in A\) and \(y \in B\}\)
- \(A\text{\textbar}B = \{x\text{\textbar}x \in A\) or \(x \in B\}\)
- \(A^* = \{x_1\cdot{x_2}\cdot{x_3}\cdot{...}\cdot{x_k}\text{\textbar}k\geq 0\) and each \(x_i \in A\}\)
are also RegExp.
It is also possible to use the following notation:
\(A^+ = \{x_1\cdot{x_2}\cdot{x_3}\cdot{...}\cdot{x_k}\text{\textbar}k\geq 1\) and each \(x_i \in A\}\)
Exercises (1) #
Consider the alphabet \(\Sigma = \{0, 1\}\) . Give English descriptions of the languages of the following regular expressions.
- \(\emptyset\) ;
- \(\emptyset{^*}\) ;
- \((0 ^ \ast 1 ^ \ast )^\ast 000 ( 0 \text{\textbar} 1 )^\ast\) ;
- \((1\text{\textbar}\epsilon)(00^\ast 1)^\ast 0^\ast\) ;
Exercises (2) #
Consider the alphabet \(\Sigma = \{a, b\}\) . Build Regular Expressions for: 5. The set of strings that consist of alternating \(a\) ’s and \(b\) ’s; 6. The set of strings that contain an odd number of \(a\) ’s; 7. The set of strings that end with \(b\) and do not contain the substring \(aa\) ; 8. The set of strngs in which both the number of \(a\) ’s and the number of \(b\) ’s are even.
Homework on NDFSA #
A. Construct NDFSAs over alphabets \(\Sigma_1 = \{a, b\}\) and \(\Sigma_2 = \{0, 1\}\)
- \( L_0 = \{x \in \Sigma_2^\ast \mid\) any \(0\) in \(x\) is followed by at least a \(1\}\) .
Strings examplle: \(010111\) , \(1111\) , \(01110111011\)
\( L_1 = \{x \in \Sigma_1^\ast \mid x\) contains the substring \(abbaab\}\) .
\( L_2 = \{x \in \Sigma_1^\ast \mid |x| \geq 2 \wedge \) final two symbols are the same \(\}\) .
\( L_3 = \{x \in \Sigma_2^\ast \mid x\) contains exactly \(5\) zeros \(\}\) .
B. Convert NDFSAs from part A to DFSAs applying the algorithm presented in the lab.